Lets start with
M = 5 8
17 3
and modulo 26.
1. Calculate inverse matrix
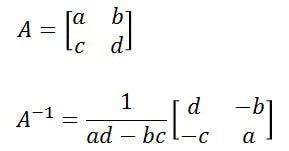
det(M) = 5*3 - 8*17 = -121
MI = 1 | 3 -8 |
---- * | -17 5 |
-121
= ?
2. How to deal with fractional number
- Apply modulo to each element in the inverse matrix.
- So we want to solve
- (3 / -121) mod 26
- = -3 * 121^(-1) mod 26
- To evaluate 121^(-1), we should calculate Modular Inverse.
3. What is Modular Inverse?
In a number system without modulo...
- If ax = 1, then x is a multiplicative inverse.
- x = 1/a. easy.
In a number system with modulo...
If ax ≡ 1 mod M, then x is a modular multiplicative inverse and x ≡ a^(-1) mod M.
- tedious but solvable.
Let's try 3x ≡ 1 mod 5.
- 3 * 0 ≡ 0 (x)
- 3 * 1 ≡ 3 (x)
- 3 * 2 ≡ 1 (o)
- x ≡ 3^(-1) ≡ 2.
For better solution, take a look at Extended Euclidean Algorithm.
4. Extended Euclidean Algorithm
- this is just for an introduction.
Euclidean Algorithm
- is an algorithm to calculate greatest common divisor. (a.k.a. GCD)
Extended Euclidean Algorithm
is an algorithm to calculate GCD and x, y from Bezout's identity.
Bezout's identity?
- If GCD(a,b)=d, then ax + by = d has a solution x and y.
Tracking Euclidean Algorithm...
- a = b * q[0] + r[1]
- b = r[1] * q[1] + r[2]
- r[1] = r[2] * q[2] + r[3]
- ...
- r[i-1] = r[i] * q[i] + r[i+1]
- => r[i+1] = r[i-1] - r[i] * q[i]