Solution

1. analytical solution
2. numerical methods

Error Types

1. Round-Off Error
   • computers can represent quantities with a finite number of digits
2. Truncation Error
   • approximate solution

Significant Digits

• is the number of certain digits plus one estimated digit.
• Zeros are not always significant figures. They are just to locate a decimal point.
  • 0.00001845 -> four
• Four signicant figures may be acceptable.
• Omission of the remaining significant figures is called round-off error.

Error

1. True error;
2. True percent relative error;
3. Approximation error
   • In real-world, we will obviously not know the true answer.
   • continue approximation until e < prespecified acceptable level.
4. (Scarborough, 1966) We can be assured that the result is correct to at least n significant figures if the approximation error falls below:

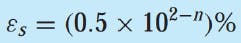
Floating-Point

Representation

• m b^e
  • m : matissa
  • b : base of the number system
  • e : exponent

• example: 7 bits
  • [0] : sign of number
  • [1] : sign of exponent
  • [2-3] : magnitude of exp
  • [4-6] : magnitude of mantissa
  • number range : 0011001 (1e-3) ~ 1111111 (7e+3)

Approximation

• Rounding
  • nearby value
• Chopping
  • discard remains

Error

• Quantizing errors
  • Overflow
  • Underflow

Quantizing Errors

• machine epsilon : ε = b^(1-t)
  • b : number base
  • t : the number of mantissa bits

Subtractive Cancellation

• round-off induced when subtracting two nearly equal floating-point numbers
• 
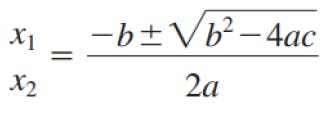
  • subtractive cancellation occurs where b^2 >> 4ac